数独是一种非常流行的数字填充游戏游戏。在数独中，玩家须以数字填满一个9x9的网格，使得其每行、每列和每个宫（即3x3的大格）都有齐1至9所有数字。游戏设计者会提供一部分的数字，使谜题只有一个答案。数独是一种逻辑性较强的益智类游戏，可以帮助训练我们的思维能力。如果使用计算机来解决数独的问题，一般可以采用深度优先搜索等方法得到答案，但是今天我们来讲讲如何通过图结构帮助我们解决这个问题。

1 图着色问题

首先，我们需要了解图着色问题(Graph coloring)。一般来讲，图着色指的是对无向图中每一个顶点赋予一种颜色，使得任何相邻两个顶点的颜色都不相同。经典的四色问题本质就是图着色问题。

图1展示了使用三种颜色对佩特森图进行着色。我们将这种对于顶点进行着色的问题称为顶点着色(Vertex coloring)，除此之外，我们还将对于边进行着色的问题称为边着色(Edge coloring)。在本文中，我们主要关注顶点着色。若我们使用$k$种颜色对图进行着色，则这种着色便被称作k-着色(k-coloring)，例如图1即为对于佩特森图的“3-着色”。对于一个最大度数为$d$的无向图，我们需要不超过$d+1$种颜色即可完成对图的着色。然而对给定图完成着色所需的颜色数目的最小值就是该图的色数(Chromatic number)。求一个图的色数是一个NP-完全问题，目前没有多项式时间内的算法。

2 贪心算法为图着色

利用贪心算法可以快速的完成图着色。该算法非常容易理解，具体Python实现如下：

import networkx as nx
from itertools import count

def graph_color(G):
    for node in G.nodes_iter():
        neighbors_color = set(G.node[neighbor]['color'] for neighbor in G.neighbors_iter(
            node) if 'color' in G.node[neighbor])
        if not neighbors_color:
            color = 0
        else:
            for color in count():
                if color not in neighbors_color:
                    break
        G.node[node]['color'] = color

    return G

我们对每一个顶点赋值一个整数$0,1,2...$来表示它的颜色。在贪心算法中，我们依次历遍每一个顶点，简称该顶点相邻所有顶点的颜色，然后对该顶点赋予一个和相邻顶点颜色不重复的最小颜色。其实我们不需要自己实现这个算法，因为NetworkX中已经包含了greedy_color的算法。需要注意的是使用贪心算法着色可以保证使用的颜色数不超过$d+1$种，并且贪心算法着色所需的颜色数被称作图的贪心着色数(Grundy number)。

3 图着色和数独

正如开头所说，我们借助图论来解数独，关键就是将数独转化为图着色问题。为了简化说明，我们先以4x4的数独为例如下图2。

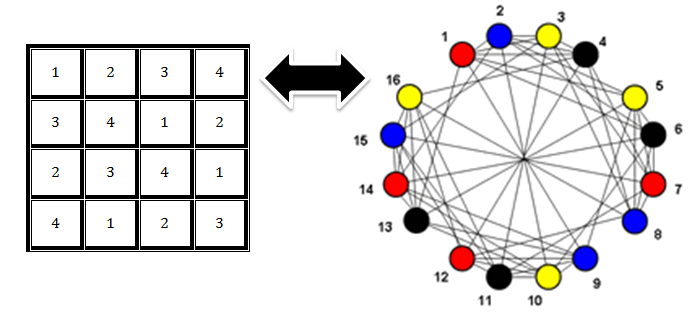
我们把数独中每一个格子看做一个顶点，并且连接同在一行，一列，或者一个宫的任意两个顶点。如果我们能对该图进行4-着色，则我们就解决了数独问题。同样我们可以将该方法扩展到9x9的网格或者其他尺寸。对于数独，一些格子中的数字已经被提供了，则我们可以将相对应的顶点看做是已经着上了某种颜色。但是需要注意的是，例如在4x4的数独中，对应的图的最大度数为$7$，所以使用贪心算法只能保证使用的颜色不超过$8$种而并不能保证只采用$4$种颜色。所以贪心算法还不足够解决所有的数独问题，我们还需要配合其它更加先进的着色算法才能完美解决数独问题。除了解决数独问题，图着色在现实生活中还有许多应用，例如铁路调度，时间表安排等等。如何快速高效的对图（尤其是大规模的图）进行着色也是一个非常热门的问题。除此之外，值得一提的是数独也是一个NP-完全问题，更多在Python中有关数独问题建模和解决的介绍可以查看Modeling Sudoku Puzzles with Python这篇文章。