(算法)单词拼接

今天接触一道有关图论的算法题目，题目如下：

给你一些单词，请你判断能否把它们首尾串起来串成一串。前一个单词的结尾应该与下一个单词的首字母相同。

样例输入：

['aloha','dog','arachnid','gopher','tiger','rat']

样例输出：

'aloha.arachnid.dog.gopher.rat.tiger'

虽然已经提到了这道题是有关图论的，但是很明显最容易实现的方法便是暴力求解了。具体方法是通过利用Python中的permutations方法生成所以这些单词所有的组合方式，然后再检查是否符合首尾相接的添加。

from itertools import permutations

def wordsJointBrute(words):
    for p in permutations(words):
        if checkJoint(p):
            return '.'.join(p)
    return None


def checkJoint(words):
    for i in xrange(len(words) - 1):
        if words[i][-1] != words[i + 1][0]:
            return False
    return True

如上方法非常容易实现，但是运行复杂度为O(n*n!)，效率非常低。接下来要考虑的是如何通过图来更好地解决这个问题。首先可以将这些单词表示为一个有向图，单词既可以表示为图中的边，也可以表示为顶点。如下例子1中左图将每个单词表示为一条边，而每个顶点则表示首尾字母。然而如下例子1右图中，每个顶点都代表一个单词，而它们之间的边表示单词首尾字母之间的关系。

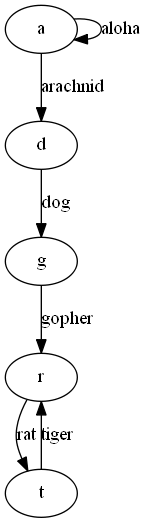
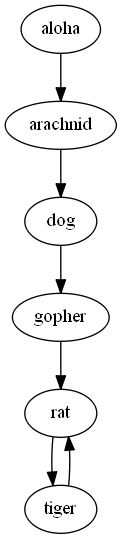
再看一组例子2 ['apple', 'alice', 'era', 'aloha']:

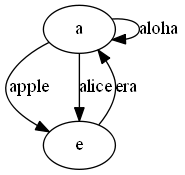
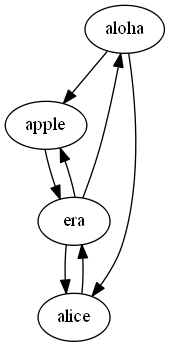
如果将单词表示为边，于是问题就是是否存在一条路径，可以遍历图中每一条边且无重复，这个路径在图论中被称为欧拉路径。如果将单词表示为点，于是问题就是是否存在一条路径，可以遍历图中每一个点且无重复，这个路径在图论中被称为哈密顿路径。寻找图中的哈密顿路径属于NP完全问题，没有很好的多项式时间内的算法，所以接下来将采取第一种策略：将单词表示为有向图中的边并寻找图中的欧拉路径。

由于要在Python中使用图结构，我们在程序中使用NetworkX库以方便算法的实现。其实上面例子中所用的图也是通过NetworkX结合PyDotPlus绘制的。需要注意的是，如果欧拉路径的起点和终点是同一个顶点，那么这样的路径便被称为欧拉回路。在NetworkX中已经包含了eulerian_circuit方法求欧拉回路。但是这道题目中并不需要路径的起点和终点是同一个顶点，所以我们使用同样的算法自己实现了寻找欧拉路径的方法，该算法可以在线性时间内完成。代码如下：

import networkx as nx

def wordsJoint(words):
    return findEulerianPath(wordsToEdges(words))


def wordsToEdges(words):
    G = nx.MultiDiGraph()
    G.add_edges_from([(word[0], word[-1], {'label': word}) for word in words])
    return G


def findEulerianPath(G):

    # Verify that graph is connected 
    if not nx.is_weakly_connected(G):
        return None

    # Check if Euler path exist
    start = None
    end = None
    count = 0

    for vertex in G.nodes_iter():
        indeg = G.in_degree(vertex)
        outdeg = G.out_degree(vertex)
        if indeg != outdeg:
            if indeg - outdeg == 1 and start is None:
                start = vertex
                count += 1
            elif outdeg - indeg == 1 and end is None:
                end = vertex
                count += 1
            else:
                return None

    # Find Euler path
    g = G.__class__(G)  # copy graph structure (not attributes)
    if count == 0:
        start = next(g.nodes_iter())

    vertex_stack = [start]
    last_vertex = None
    path = []

    while vertex_stack:
        current_vertex = vertex_stack[-1]
        if g.in_degree(current_vertex) == 0:
            if last_vertex is not None:
                data = G.get_edge_data(last_vertex, current_vertex)
                key, value = data.popitem()
                path.append(value['label'])

            last_vertex = current_vertex
            vertex_stack.pop()
        else:
            random_edge = next(g.in_edges_iter(current_vertex))
            vertex_stack.append(random_edge[0])
            g.remove_edge(*random_edge)

    return '.'.join(path)