隐马尔可夫模型（Hidden Markov Model，HMM）是一种基本的统计模型，最早在上世纪80年代被提出，可以被应用在语音识别，自然语言处理，生物信息，模式识别等等领域。虽然目前神经网络在一些方面已经取代了隐马尔可夫模型，隐马尔可夫模型依旧是机器学习中非常重要并且值得学习的一个模型。

1 模型定义

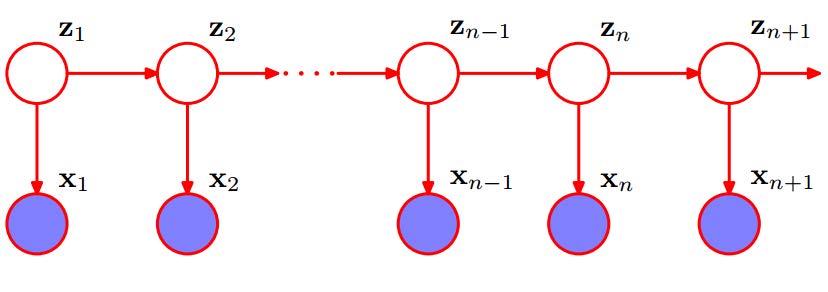
隐马尔可夫模型用来描述一个含有隐含未知参数的马尔可夫过程(Markov chain)。其中，马尔科夫过程是指一个未来状态的条件概率分布仅依赖于当前状态的随机过程。也就是说，隐马尔可夫模型是关于时序的概率模型，描述由一个隐藏的马尔科夫链生成不可观测的状态随机序列，再由各个状态生成观测随机序列的过程。

如图1中，$Z_i$为状态随机序列，简称状态序列。$X_i$为状态序列生成的观测随机序列，简称观测序列。状态序列$Z_i$满足马尔科夫过程的要求，并且观测序列$X_i$受制于$Z_i$。在$Z_i$不可知的情况下，该模型中的$X_i$与$X_{i+1}$是不独立的。

2 模型参数

隐马尔可夫模型由初始概率分布$\pi$、状态转移概率分布$A$以及观测概率分布$B$确定。若我们用字母$\lambda$来表示一个隐马尔科夫模型，则可写作$\lambda=(A,B,\pi)$。

对于状态序列和观测序列可能出现的值，我们表示如下：

• $Q$是所有可能的状态的集合，$Q={q_1,q_2,···,q_N}$

• $V$是所有可能的观测的集合，$V={v_1,v_2,···,v_M}$

可以发现，$N$是可能的状态数，而$M$是可能的观测数。事实上，在少数情况中，$V$可能是一个连续的分布而不是离散的集合，我们暂时不考虑这种情况。

紧接着，我们用$I$表示长度为$T$的状态序列，即$I={i_1,i_2,...,i_T}$。$O$则表示对应的观测序列，即$O={o_1,o_2,...,o_T}$。

那么，状态转移概率矩阵$A$为

$$A=[a_{ij}]{N \times N} \quad \textrm{where} \quad a=P(i_{t+1}=q_j|i_t=q_i)$$

即$a_{ij}$是在时刻$t$处于状态$q_i$的条件下时刻$t+1$转移到状态$q_j$的概率。

除此之外，状态转移概率矩阵$B$为

$$B=[b_{ik}]{N \times M} \quad \textrm{where} \quad b=P(o_t=v_k|i_t=q_i)$$

即$b_{ik}$是在时刻$t$处于状态$q_i$的条件下生成观测$v_k$的概率。

最后，$\pi$是初始状态概率向量

$$\pi=(\pi_i)_N \quad \textrm{where} \quad \pi=P(i_1=q_i)$$

也就是说，$\pi_i$是时刻$t=1$时处于状态$q_i$的概率。

3 基本性质

不难看出，隐马尔科夫模型有两个基本性质：

• 齐次假设

$$P(i_t|i_{t-1},o_{t-1},i_{t-2},o_{t-2},...,i_1,o_1)=P(i_t|i_{t-1})$$

• 观测独立性假设

$$P(o_t|i_{T-1},o_{T-1},i_{T-2},o_{T-2},...,i_1,o_1)=P(o_t|i_t)$$

4 总结

以上便是隐马尔科夫模型的基本介绍，但在实际运用中，我们常常涉及到3个基本问题。它们分别是概率计算问题（前向-后向算法等），学习问题（Baum-Welch算法等），以及预测问题（Viterbi算法等）。这些会在以后的文章中介绍到。