链接分析(Link analysis)是指对对网络结构中超链接(Hyperlinks)进行分析。链接分析在网络搜索引擎技术中有着重要的地位，我们可以利用其判断网页的重要性以及它们和搜索关键词的相关度来由此对搜索结果进行排名。在本文中，我简单的介绍PageRank算法与HITS算法两种经典的链接分析算法。

1 基本假设

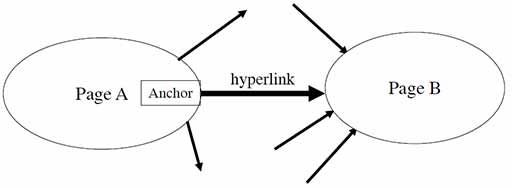
如图1所示，在链接分析中我们用有向图来表示网页之间的关系。在这个模型中，我们常常有两个假设：

• 指向页面的超链接代表着页面的权威性(Authority)

• 超链接中的锚文本(Anchor text)描述了目标页面的内容

所谓的锚文本即超链接中的文字。正常情况下，锚文本能比目标网页中的文本更好地描述该网页的内容。所以在搜索引擎中的索引中，锚文本的权重往往比文档本身要高。除此之外，对于锚文本的权重也不一定是唯一的，例如对于权威网站(如cnn.com)中的锚文本，我们可以给予比一般锚文本更高的权重。但是锚文本索引的方法也存在一定的缺点，恶意的攻击者可以利用锚文本高权重的特点制作大量不合事实的锚文本超链接来恶意提高特定网页的搜索排名。在历史上曾出现的Google轰炸(Google bomb)便是利用这种方法实现的，但随着Google在2007年初改进了其排名算法，这种Google轰炸也慢慢销声匿迹了。

2 PageRank

回到正题，PageRank[ref]The PageRank Citation Ranking: Bringing Order to the Web[/ref]是由Google在1998年正式提出的，PageRank这个名字也是以其提出者，Google创始人之一的Larry Page的而命名的。PageRank受到了早期引文分析(Citation analysis)的影响，也是Google如今能如此成功的奠基石。

要理解PageRank，我们首先需要想象一个浏览者在随机地浏览网页。假设该浏览者从一个随机的网页开始浏览，并且在每一个步中，都以相同的概率点击网页上的任意一个超链接进入下一个网页。在这个随机过程中，非常明显的是下一个将要浏览的网页的概率只与当前网页（中的超链接情况）有关。这便是一个常见的马尔可夫链(Markov chain)，链中的每一个状态便是随机浏览到的一个网页。由此，我们可以构建出一个转移矩阵(Stochastic matrix)$P$，该矩阵中的元素$P_{ij}=P(j|i)$，即当浏览者浏览完毕网页$i$下一个将会打开网页$j$的概率。回顾我们的假设，任一页面中每个超链接被点击到的概率是相等的，我们以图2中的网络举例说明。

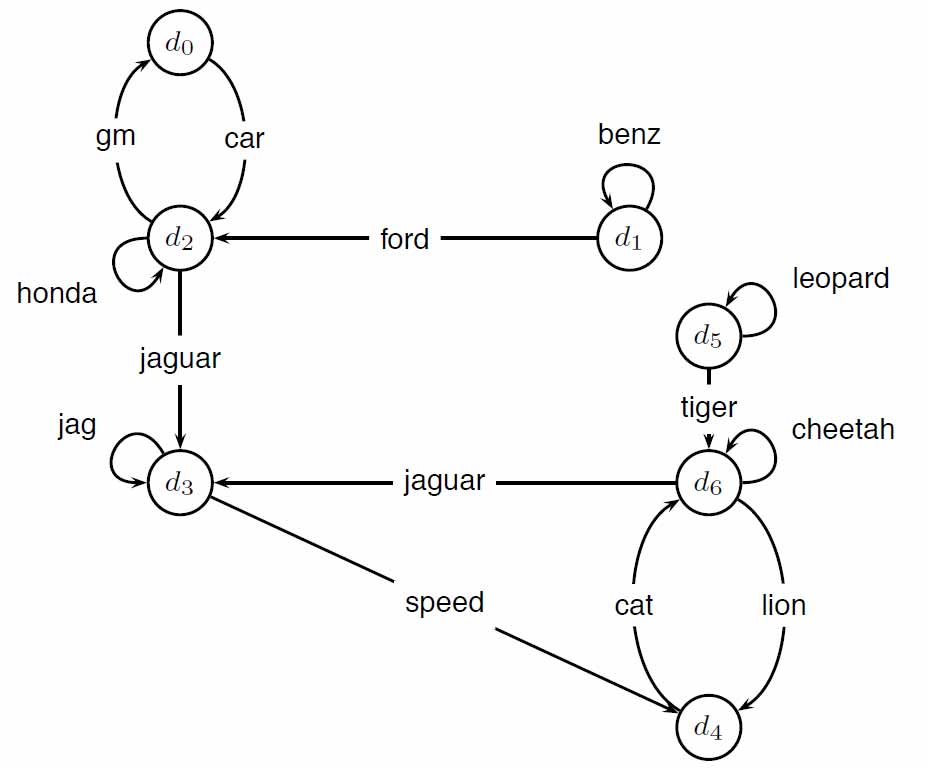
得到转移矩阵$P$如下：

$$P= \begin{bmatrix} 0.00 & 0.00 & 1.00 & 0.00 & 0.00 & 0.00 & 0.00\ 0.00 & 0.50 & 0.50 & 0.00 & 0.00 & 0.00 & 0.00\ 0.33 & 0.00 & 0.33 & 0.33 & 0.00 & 0.00 & 0.00\ 0.00 & 0.00 & 0.00 & 0.50 & 0.50 & 0.00 & 0.00\ 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 1.00\ 0.00 & 0.00 & 0.00 & 0.00 & 0.00 & 0.50 & 0.50\ 0.00 & 0.00 & 0.00 & 0.33 & 0.33 & 0.00 & 0.33 \end{bmatrix}$$

每一个网页的PageRank值就是当我们不断重复上述随机浏览的过程时，该网页会被访问到的概率。而一个网页在随机访问中被访问到的概率越高，则它就越重要。我们需要重复大量随机访问来得到如上所述的概率。

但是在实际真实的网络中，可能存在一些不存在任何超链接或者没有被任何网页指向的页面，访问者在访问这样的网页后无法通过其中的超链接进入下一个网页。为了防止这种情况，我们加入额外的阻尼系数(Damping factor)的概念。即在访问完一个不含任何超链接的网页后，我们让浏览者随机跳转到网络中任何一个网页，而在访问其他页面时，我们让浏览者有$1-d$的概率随机跳转到网络中任何一个网页，$d$的数值便是阻尼系数。根据统计，我们一般选取$d=0.85$。阻尼系数出现后，上图2中所示网络的转移矩阵$P$就变成了：

$$P= \begin{bmatrix} 0.02 & 0.02 & 0.88 & 0.02 & 0.02 & 0.02 & 0.02\ 0.02 & 0.45 & 0.45 & 0.02 & 0.02 & 0.02 & 0.02\ 0.31 & 0.02 & 0.31 & 0.31 & 0.02 & 0.02 & 0.02\ 0.02 & 0.02 & 0.02 & 0.45 & 0.45 & 0.02 & 0.02\ 0.02 & 0.02 & 0.02 & 0.02 & 0.02 & 0.02 & 0.88\ 0.02 & 0.02 & 0.02 & 0.02 & 0.02 & 0.45 & 0.45\ 0.02 & 0.02 & 0.02 & 0.31 & 0.31 & 0.02 & 0.31 \end{bmatrix}$$

我们用向量$\vec{x}=(x_1,x_2,...,x_n)$来表示随机浏览的过程中某一时刻每个网页被访问到的概率。假设我们从网页$i$开始访问，则$\vec{x}=(\underset{0}{0},...,\underset{i}{1}，...,\underset{n}{0})$。这里起始网页的选择和最终PageRank结果完全无关。在回顾一下转移矩阵的定义就可以发现，下一步我们的概率向量$\vec{x}=\vec{x}P$，紧接着将会变为$\vec{x}P^2$，$\vec{x}P^3$以此类推。当进入稳定状态时，$\vec{x}$的值将不再发生变化，我们把稳定状态下的概率向量$\vec{x}$重新用$\vec{a}$表示，$\vec{a}$就是我们想要得到的每个网页的PageRank的值。和上面概率的变化类似，当前状态$\vec{a}$的下一个状态下的概率向量为$\vec{a}P$，但是由于$\vec{a}$不会改变，所以$\vec{a}=\vec{a}P$。由此我们便得出了结论——PageRank值的向量$\vec{a}$是转移矩阵$P$的（主）特征向量。这被称作马尔可夫链的不变分布(Stationary Distribution)。实践中，我们通常用幂迭代法(Power iteration)来求解，也就是让$\vec(a)$不断乘以$P$的幂直到误差小于我们的要求。图2网络PageRank结果计算如下：

	$\vec{x}$	$\vec{x}P$	$\vec{x}P^2$	$\vec{x}P^3$	$\vec{x}P^4$	$\vec{x}P^5$	$\vec{x}P^6$	$\vec{x}P^7$	$\vec{x}P^8$	$\vec{x}P^9$	$\vec{x}P^{10}$	$\vec{x}P^{11}$	$\vec{x}P^{12}$
d0	0.14	0.06	0.09	0.07	0.07	0.06	0.06	0.06	0.06	0.05	0.05	0.05	0.05
d1	0.14	0.08	0.06	0.04	0.04	0.04	0.04	0.04	0.04	0.04	0.04	0.04	0.04
d2	0.14	0.25	0.18	0.17	0.15	0.14	0.13	0.12	0.12	0.12	0.12	0.11	0.11
d3	0.14	0.16	0.23	0.24	0.24	0.24	0.24	0.25	0.25	0.25	0.25	0.25	0.25
d4	0.14	0.12	0.16	0.19	0.19	0.20	0.21	0.21	0.21	0.21	0.21	0.21	0.21
d5	0.14	0.08	0.06	0.04	0.04	0.04	0.04	0.04	0.04	0.04	0.04	0.04	0.04
d6	0.14	0.25	0.23	0.25	0.27	0.28	0.29	0.29	0.30	0.30	0.30	0.30	0.31

为了保证算法收敛得到唯一的值全为正数的向量，转移矩阵必须是随机的(Stochastic)，不可约的(Irreducible)，和非周期的(Aperiodic)，而在引入了阻尼系数后，算法中的转移矩阵满足以上条件。总结起来，为了计算PageRank，我们需要构建转移矩阵$P$然后求解特征向量$\vec{a}$即可。$\vec{a}$中的值即是网页的PageRank且值的范围都在$0$到$1$之间。我们可以发现PageRank是与搜索的关键词无关的，所以所以计算均可离线操作。在PageRank中，被指向的次数越多，被PageRank越高的网站指向的网页就会有越高的分值。但是PageRank的缺点也很明显：第一，随机行走的模型不符合现实中人们的行为；第二，没有对于内链和其他低价值链接进行过滤；第三，无法衡量与搜索关键字的相似度；第四，对于高质量的新网页不友好。由于以上缺点，PageRank已经不是主流搜索引擎目前排序的主要依据了，但在爬虫规则等方面依据占据着重要的地位。

3 HITS

HITS (Hyperlink-Induced Topic Search)[ref]Authoritative Sources in a Hyperlinked Environment[/ref]算法则是从一个有些不同的角度来对网页进行排序。HITS算法主要关注网络中的权威页面(Authority)和枢纽页面(Hub)。权威页面顾名思义指的是一些重要的高质量页面，而枢纽页面指的是有很多指向权威页面的链接的页面。HITS算法主要基于一些两个假设：

• 一个高质量的权威页面会被很多高质量的枢纽页面所指向。

• 一个高质量的枢纽页面会指向很多高质量的权威页面。

可以发现这个定义其实是相互递归相互影响，我们可以使用迭代计算的方法来进行计算。对于网络中每一个页面，我们都赋予它一个Authority值$a$和Hub值$h$。HITS算法对于泛指主题检索提问(Broad-topic queries)较为有效。

为了计算HITS值，我们从一个初始集合(Base set)开始，根据以上假设不断迭代更新$a$和$h$的值直至稳定状态。给出一个查询，例如查询“计算机”，首先我们通过索引查找出所以包含关键字“计算机”的页面。这些包含关键字“计算机”的页面的集合被称为根集合(Root set)。然后我们将所以指向根集合中任意网页或者被根集合中任意网页指向的网页也添加进集合中，这便构成了初始集合。以下图示3很好的展示了根集合和初始集合的关系。

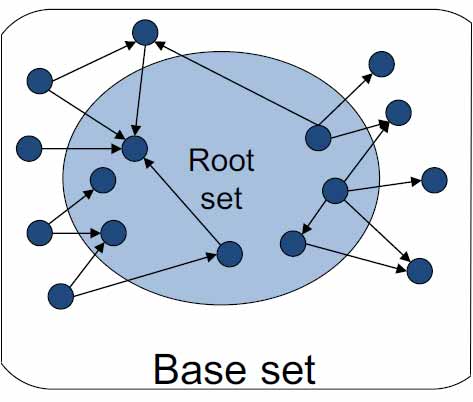
对于任一页面$d$，我们首先初始化$a(d)=1$，$h(d)=1$，然后不断迭代更新$a(d)$和$h(d)$的值。更新的规则为页面hub值等于所有它指向的页面的authority值之和，页面authority值等于所有指向它的页面的hub值之和。

如图4所示，更新的过程可以写作：

$$h(d) \leftarrow \sum_{\forall d':d \mapsto d'} a(d')$$

$$a(d) \leftarrow \sum_{\forall d':d \mapsto d'} h(d')$$

为了防止hub值和authority值在不断更新中值变得过大，我们可以在每轮更新后按比例缩小(Scale down)所有的数值。因为我们只需要知道数值之间的相对关系，所以缩小的比例因子(Scale factor)的值不会影响最终的结果。一般在实际运用中，只需要较少次数的迭代数值就会进入稳定的状态。

我们用矩阵$A$表示初始集合的邻接矩阵(Adjacency matrix)，并且将所以页面的hub和authority值表示为向量$\vec{h}$和$\vec{a}$。那么我们可以得到：

$$\vec{h}=\lambda A \vec{a}$$

$$\vec{a}=\mu A^T \vec{h}$$

其中常数$\lambda$和$\mu$均为Scale的比例因子。由此可得：

$$\vec{h}=\lambda \mu A A^T \vec{h}$$

$$\vec{a}=\lambda \mu A^T A \vec{a}$$

所以当算法收敛时，$h$便是$AA^T$的（主）特征向量，而$a$则是$A^TA$的（主）特征向量。和PageRank类似，我们可以用幂迭代法求解。还是以图2为例，该网络的邻接矩阵$A$如下:

$$A= \begin{bmatrix} 0 & 0 & 1 & 0 & 0 & 0 & 0\ 0 & 1 & 1 & 0 & 0 & 0 & 0\ 1 & 0 & 1 & 2 & 0 & 0 & 0\ 0 & 0 & 0 & 1 & 1 & 0 & 0\ 0 & 0 & 0 & 0 & 0 & 0 & 0\ 0 & 0 & 0 & 0 & 0 & 0 & 1\ 0 & 0 & 0 & 0 & 0 & 1 & 1 \end{bmatrix}$$

用幂迭代法求解$h$过程如下：

	$\vec{h}_0$	$\vec{h}_1$	$\vec{h}_2$	$\vec{h}_3$	$\vec{h}_4$	$\vec{h}_5$
d0	0.14	0.06	0.04	0.04	0.03	0.03
d1	0.14	0.08	0.05	0.04	0.04	0.04
d2	0.14	0.28	0.32	0.33	0.33	0.33
d3	0.14	0.14	0.17	0.18	0.18	0.18
d4	0.14	0.06	0.04	0.04	0.04	0.04
d5	0.14	0.08	0.05	0.04	0.04	0.04
d6	0.14	0.30	0.33	0.34	0.35	0.35

同时，求解$a$过程如下：

	$\vec{a}_0$	$\vec{a}_1$	$\vec{a}_2$	$\vec{a}_3$	$\vec{a}_4$	$\vec{a}_5$	$\vec{a}_6$
d0	0.06	0.09	0.10	0.10	0.10	0.10	0.10
d1	0.06	0.03	0.01	0.01	0.01	0.01	0.01
d2	0.19	0.14	0.13	0.12	0.12	0.12	0.12
d3	0.31	0.43	0.46	0.46	0.46	0.47	0.47
d4	0.13	0.14	0.16	0.16	0.16	0.16	0.16
d5	0.06	0.03	0.02	0.01	0.01	0.01	0.01
d6	0.19	0.14	0.13	0.13	0.13	0.13	0.13

相比较PageRank，HITS计算效率较低，这是因为我们不可以离线计算HITS值，必须要在每次查询时计算一次。除此之外，主题漂移(Topic drift)也是HITS算法存在的一大问题。主题偏移指的是在从根集合扩展到初始集合时，一些其他主题的高权威页面可能会被包含进来，这些网站会出现在搜索结果的前列但并不是浏览者想要看到的。还有就是作弊网页的问题，一个作弊网页只要设计很多指向高Authority值的页面便可以成为一个高质量的Hub，然后继续添加指向自己的链接就可以同时成为高权威的页面。而且由于HITS算法计算过程中只在整个网络图中的一个子图中进行，相对较小的图规模使得其很容易收到垃圾链接的影响。

4 总结

一个网页的PageRank分值与指向该网页的网站有关，而HITS分值则还与该网页指向的其他网站有关。从模型定义和计算复杂度等等方面，PageRank算法和HITS算法各有所长。在下一篇中，我们将介绍面向主题的PageRank (Topic-sensitive PageRank)算法以及可以用来识别垃圾网页的TrustRank。

5 参考资料