1 题目描述

外星人有自己的语言。虽然他们使用的字母表和英文相同，但是字母的顺序不同。现在你截获了一部外星人的字典，字典中单词的顺序按照外星人的字母表顺序的规则排列。你能通过字典分析出外星人的字母顺序吗？

输入示例：

[
    "wrt",
    "wrf",
    "er",
    "ett",
    "rftt"
]

输出示例：

"wertf"

注释：

1.所有字母均为小写字母
2.如果没有合法的顺序序列，输出空串
3.如果有多个合法的顺序序列，输出任意一个即可

2 抽象为图

这道题目的技巧就是需要将字母的关系抽象为图。首先我们需要从单词的顺序中得到字母的大小关系。回忆一下字符串比较的规则，我们从左边开始一次比较一个字符，直至字符出现差异或者一个字符串结束为止。在获取字母大小关系时也是类似的，例如"wrt"和"wrf"两个单词中，从左往右第一组不同的字母为"t"和"f"，所以"t" < "f"。由于大小关系有传递性，所以我们只需要比较每组相邻的单词即可。然后我们将这些字母的关系表述为一个有向图，若字母A小于字母B，则有一条从A指向B的边。借助Python的networkX库，可以非常简单的实现转化为图的过程：

import networkx as nx


def get_edge(word1, word2):
    for a, b in zip(word1, word2):
        if a != b:
            return (a, b)
    if len(word1) > len(word2):
        raise ValueError()
    return None


def get_edges(words):
    edges = set()
    for word1, word2 in zip(words[:-1], words[1:]):
        edge = get_edge(word1, word2)
        if edge is not None:
            edges.add(edge)
    return edges


def to_graph(words):
    G = nx.DiGraph()
    G.add_edges_from(get_edges(words))
    return G

由题中示例得到图1如下：

我们再来多看几组例子。

例二：

[
    "aplw",
    "plea",
    "plwf",
    "de",
    "dac"
]

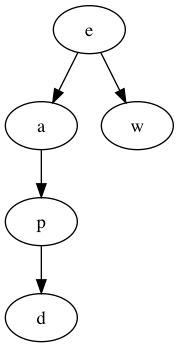
例三：

[
    "ab",
    "bbq",
    "bcw",
    "ac"
]

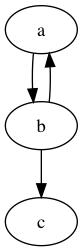
3 拓扑排序

对于题目中给出的例子来说，可以清晰的从得到的图中看出字母的顺序，然而对于额外的例二则有多种排序方式。额外的例三中的图由于存在环所有无法进行排序。这种对图中的顶点进行排序的方法叫做拓扑排序(Topological Sort)。给定一个有向无环图，拓扑排序满足如果存在一条从顶点A到顶点B的路径，那么在排序中B出现在A的后面。networkX中已经定义了拓扑排序方法，如果直接调用的话则该题的实现如下：

def get_order(words):
    try:
        G = to_graph(words)
        order = nx.algorithms.topological_sort(G)
        return ''.join(order)
    except:
        return ''

拓扑排序的复杂度一般为O(|V|+|E|)，下面我们来介绍两种常用的算法。

4 卡恩算法

卡恩算法(Kahn's algorithm)中向保存结果的列表中添加顶点的顺序和拓扑排序顺序相同。第一步是将所有入度(in-degree)为0的顶点加入一个列表（可以使用set，queue，stack等不同数据结构）中，接下来的步骤的伪代码如下：

L ← Empty list that will contain the sorted elements
S ← Set of all nodes with no incoming edges
while S is non-empty do
    remove a node n from S
    add n to tail of L
    for each node m with an edge e from n to m do
        remove edge e from the graph
        if m has no other incoming edges then
            insert m into S
if graph has edges then
    return error (graph has at least one cycle)
else 
    return L (a topologically sorted order)

点击这里可以查看算法演示。该算法的主要概念是S中的所有顶点在当前步骤下的图中都满足没有任何其它顶点指向它，所以把它添加到L中必然不会违反拓扑排序的条件。使用了networkX的Python实现如下：

def kahns_algorithm(G):
    if not G.is_directed():
        raise nx.NetworkXError(
            "Topological sort not defined on undirected graphs.")

    g = G.__class__(G)  # copy graph structure (not attributes)

    order = []
    queue = set()

    for node, in_degree in g.in_degree_iter():
        if in_degree == 0:
            queue.add(node)

    while queue:
        n = queue.pop()
        order.append(n)
        for m in g[n].keys():
            g.remove_edge(n, m)
            if g.in_degree(m) == 0:
                queue.add(m)

    if g.number_of_edges() != 0:
        raise nx.NetworkXUnfeasible("Graph contains at least one cycle.")

    return order

5 深度优先搜索算法

另一种拓扑排序则基于深度优先搜索(DFS)，该算法以和拓扑排序相反的顺序添加顶点。该算法以任意顺序对图中所有顶点展开深度优先搜索。深度优先搜索在遇到以前访问过的顶点或者叶顶点(leaf node)时终止。伪代码如下：

L ← Empty list that will contain the sorted nodes
while there are unmarked nodes do
    select an unmarked node n
    visit(n)

function visit(node n)
    if n has a temporary mark then stop (not a DAG)
    if n is not marked (i.e. has not been visited yet) then
        mark n temporarily
        for each node m with an edge from n to m do
            visit(m)
        mark n permanently
        unmark n temporarily
        add n to head of L

点击这里查看算法演示。使用了networkX的Python实现如下：

def dfs_algorithm(G):
    if not G.is_directed():
        raise nx.NetworkXError(
            "Topological sort not defined on undirected graphs.")

    def _dfs(v):
        ancestors.add(v)

        for w in G[v]:
            if w in ancestors:
                raise nx.NetworkXUnfeasible("Graph contains a cycle.")

            if w not in explored:
                _dfs(w)

        ancestors.remove(v)
        explored.add(v)
        order.append(v)

    ancestors = set()
    explored = set()
    order = []

    for v in G.nodes_iter():
        if v not in explored:
            _dfs(v)

    order.reverse()
    return order

6 总结

拓扑排序在图论中有着非常重要的地位，同时也被被广泛的运用在现实中各种不同的任务中，例如在任务调度和处理软件依赖关系等等。我们之前提到的networkx.algorithms.topological_sort中使用的算法为非递归的深度优先搜索算法。networkX也支持上述递归版的深度优先搜索算法networkx.algorithms.topological_sort_recursive。

在手机上阅读或分享本文请扫描以下二维码：

(算法)外星人的字典