支持向量机(SVM)是机器学习中一种基本的监督式学习模型。SVM最早在1963年被提出，但真正的完善应该是在90年代中期。在这期间，软间隔(Soft Margin)和核技巧(Kernel Trick)等被提出，使得SVM可以真正的被运用在现实世界中较为复杂的数据中。SVM即可以被用来完成分类(Classification)的任务，也可以实现回归(Regression)分析。虽然SVM是一种很基本的模型，但是在很多情况下效果都不错，我们以预测交通流量为例简单的介绍一下SVM在时空数据中的应用。

1 数据情况

我们使用的是London Congestion Analysis Project (LCAP)在2011年通过车牌自动识别技术在伦敦千余条道路段中收集到的数据。道路上的摄像机两两一组分别记录下车辆通过第一个摄像机和第二个摄像机的时间，从而得到车辆的行程时间。数据以5分钟为单位聚合，总共有30天，数据本身的单位为妙每米(s/m)。下图1为LCAP项目中路段的分布图。

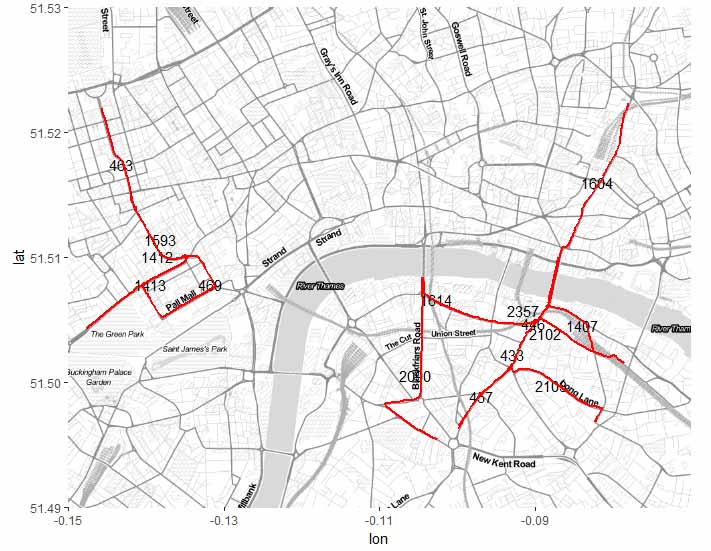
我们在以上路段中选取伦敦市中心的15条道路段，并在这个新选取出来道路网络中展开分析。选取的15条道路段如下图2所示。

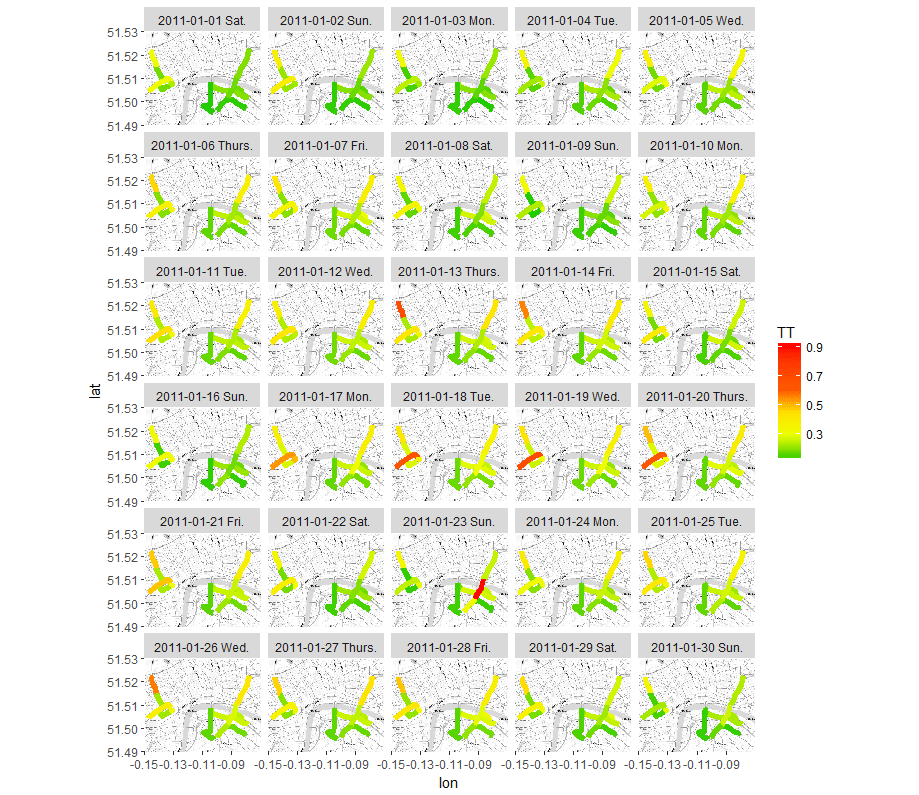
我们紧接着将道路的拥堵情况以天为单位展示在下图3。

2 时间模型

在这个例子中，我们以道路463为例，通过SVM建立一个回归模型(SVR)。数据集的前23天被用来作为训练集，后7天作为测试集。为了实现一个非线性的预测模型，我们使用常用的Gaussian radial basis function (RBF)内核。对于时间模型，我们通过前$m$个观测数据预测后一个数值。$m$的值和模型误差的关系如下图4所示。

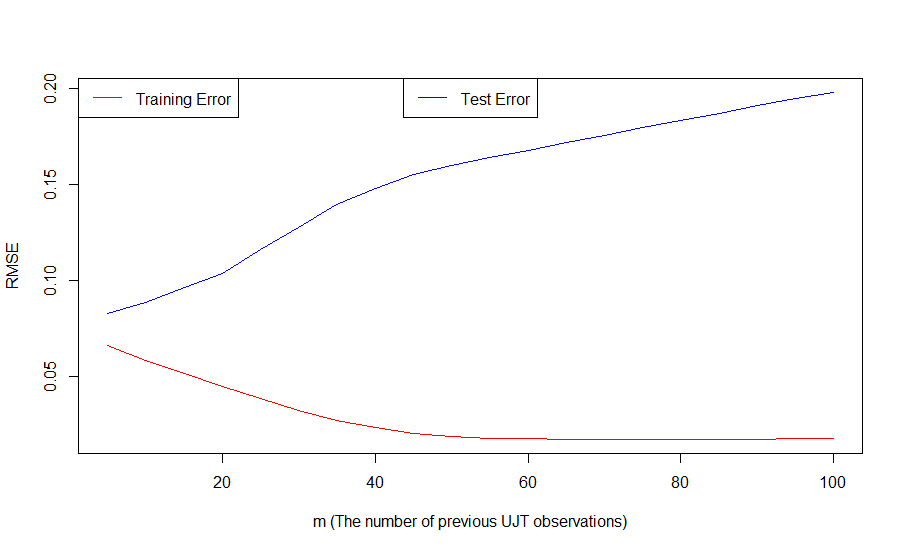
我们可以发现，随着$m$的增长，虽然训练误差不断减少，但是测试误差不断增大，这应该是由于过拟合造成的。所以在正式的模型中，我们选取$m=5$。

接下来该模型的参数主要就是SVM软间隔中的Cost($C$)和RBF中的$\sigma$。$C$主要代表错误分类所带来的损失，而$\sigma$则是RBF内核的bandwidth。接下来如图5和6所示，我们对这两个值进行两轮调参(parameter tuning)。除此之外，我们采用5-fold cross validation来减少过拟合的发生几率。

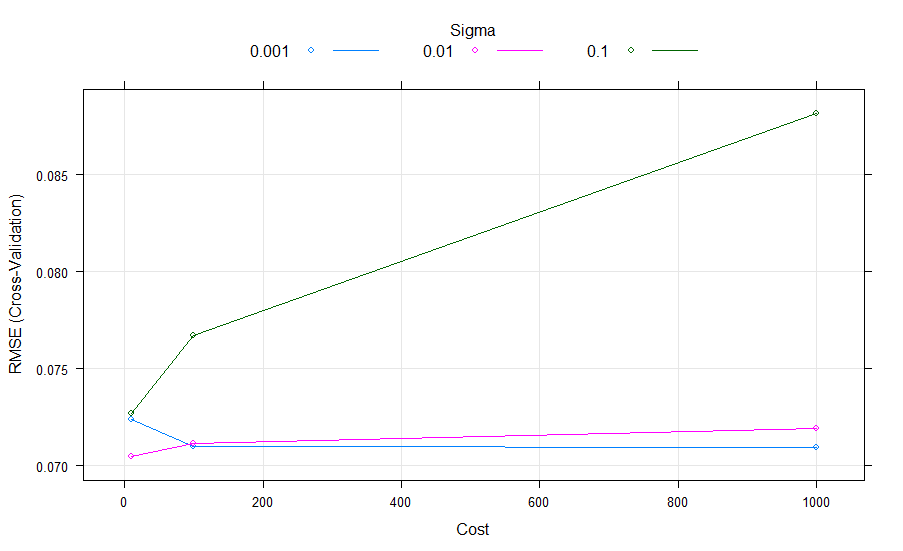
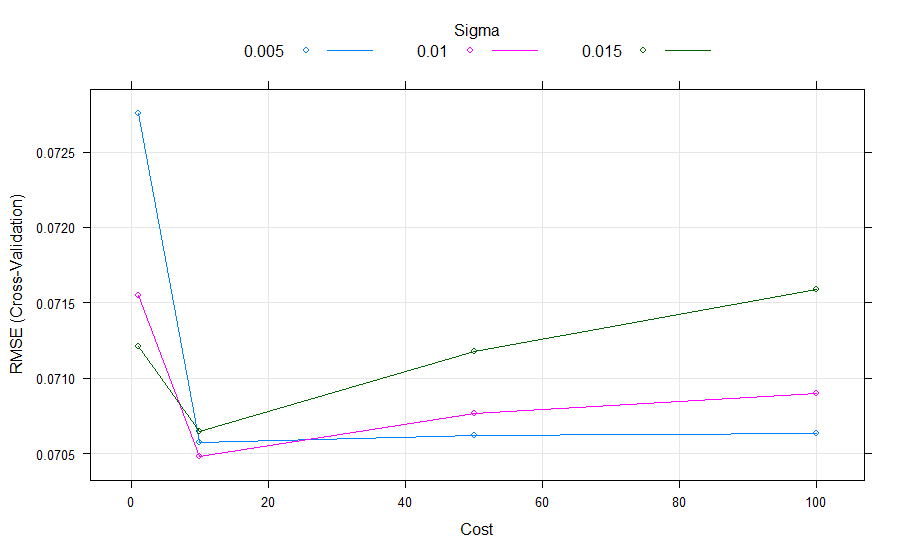
经过两轮调参，我们最终选择$C=10,\sigma=0.01$。得到最终模型后，我们通过该模型进行对后7天的预测，预测结果如下图7：

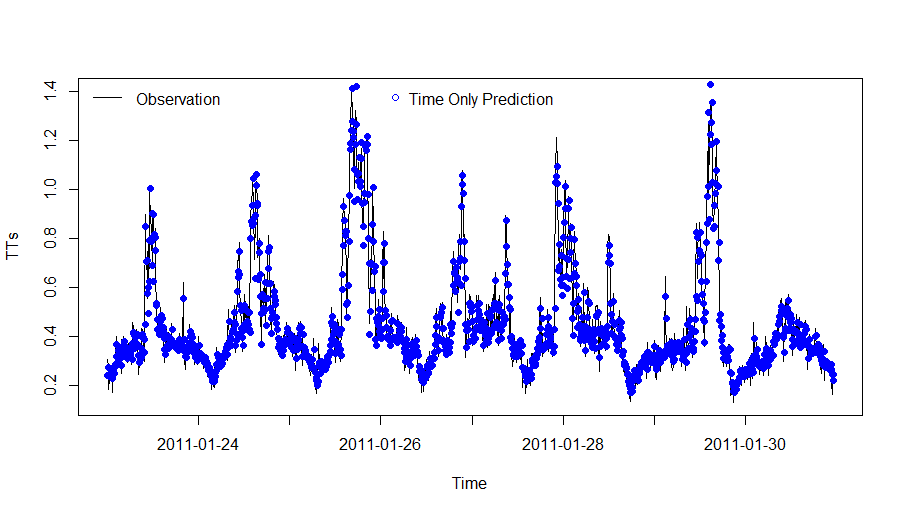
上图中蓝色点为我们的预测值，可以看出预测的准确度还不错，具体来讲，方均根差(RMSE)为$0.080$。

3 时空模型

对于预测交通情况来讲，除了时间上的关联还有空间上的关联。在这个时空模型中，我们根据子网络中的相连关系生成空间权重矩阵(Weight Matrix)，然后根据权重将相连道路上的数据添加到特征空间中。和时间模型类似，经过调参，我们选择$m=5,C=10,\sigma=0.01$。预测结果如下图8：

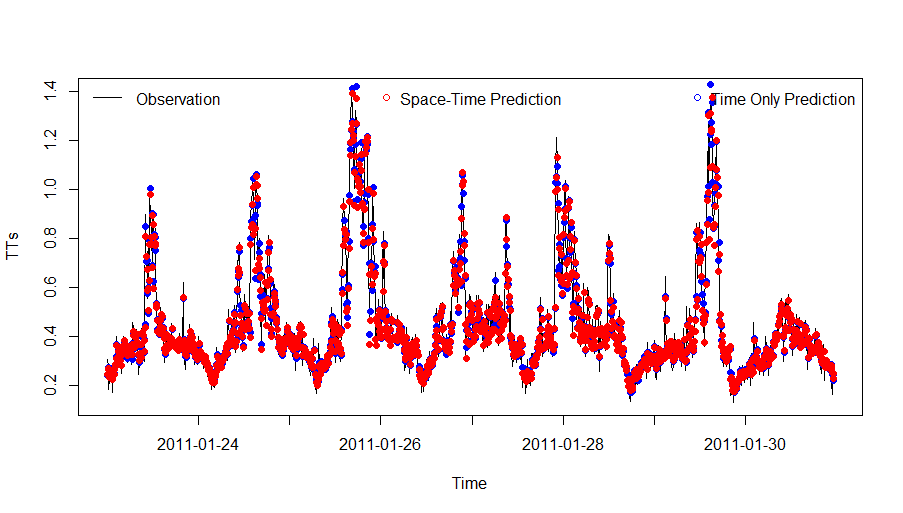
图中红点表示时空模型的预测结果，蓝点是时间模型的预测结果。从图上可以看出两个模型的表现十分接近，事实上时空模型的RMSE为$0.081$。虽然时空模型结合了更多的特征，但进步较时间模型并不大，这可能是由于与道路463相连的道路上的流量和道路463上的流量相关性不强造成的。

4 总结

以上示例大致的展现的SVM在时空数据分析中的基本应用，所有过程均通过R语言中的caret库完成。总的来说，SVM的使用非常简单，也可以提供不错的效果。

5 参考文献

Cheng, T., Haworth, J. and Wang, J. 2012. Spatio-temporal autocorrelation of road network data. Journal of Geographical Systems. 14, 4 (2012), 389–413.