找出列表中重复的元素也是算法中的老生常谈了，同时这也并不是一个很复杂的问题。但是今天的题目还有一些特殊，也很有趣。在这道题目中，我们有一个只包含整数的列表，并且这个列表满足以下两个条件：

列表中的整数范围在[1..n]中
列表的长度为n+1

可以知道，在这个列表中至少有一个整数重复出现了两次(抽屉原理)，当然也可能有很多整数重复出现并且重复的次数不止两次。我们需要找出的是哪一个整数重复出现了，如果有不止一个整数重复出现，我们只需要给出其中任意一个即可。需要注意的是，我们使用的计算机内存很小，所以给出的程序只能使用$O(1)$的内存空间。

题目说完了，再次重复一下我们的算法的空间复杂度必须为常数。不卖关子，先直接告诉大家，最优的算法能在保持常数空间使用的情况下实现$O(n)$的复杂度。虽然如此，我们还是从最基本的方法说起。

1 $O(n^2)$的解法

最简单的方法就是通过两个循环历遍去查找。Python代码如下:

def find_duplicate(int_list):
    for i, i_value in enumerate(int_list):
        for j, j_value in enumerate(int_list):
            if i != j and i_value == j_value:
                return i_value

2 $O(n\log(n))$的解法

进一步思考可以发现如果我们对列表进行in-place的排序，查找时只需要循环一遍即可。但是这种方法无法维持列表中整数原有的顺序，有没有其他的方法能实现$O(n\log(n))$的复杂度呢？回忆一下，一般满足这种复杂度的算法都使用了分治的思想，例如二分查找。那我们能不能对这道题采取类似的做法呢？直接对列表进行二分查找显然是行不通的，但是我们可以对整数的范围，即1到n，进行二分查找。首先将[1..n]从中点分成左右两个不相交的区间，然后我们对列表中属于左区间范围[1..n//2]内的整数的出现总次数进行计数。如果出现的次数大于左区间的长度，则重复的整数一定在左区间中，我们在左区间中再进行新的二分查找。反而言之如果出现的次数不大于左区间的长度，则重复的整数一定在右区间中，我们在左区间中再进行新的二分查找。反复上面步骤直至找到答案。Python代码如下：

def find_duplicate_good(int_list):
    start = 1
    end = len(int_list) - 1

    while start < end:

        # divide our range 1..n into an upper range and lower range
        midpoint = start + ((end - start) / 2)
        lower_range_start, lower_range_end = start, midpoint
        upper_range_start, upper_range_end = midpoint + 1, end

        # count number of items in lower range
        items_in_lower_range = 0
        for item in int_list:
            if lower_range_start <= item <= lower_range_end:
                items_in_lower_range += 1

        lower_range_length = lower_range_end - lower_range_start + 1

        if items_in_lower_range > lower_range_length:
            # there must be a duplicate in the lower range
            start, end = lower_range_start, lower_range_end
        else:
            # there must be a duplicate in the upper range
            start, end = upper_range_start, upper_range_end

    return start

3 $O(n)$的解法

接下来该说说$O(n)$的解法了，这种方法需要一些特别的技巧，如果没有遇到过类似的题目就很难想到了。这个技巧就是将列表中的整数当作指针来看待，通过这种映射我们得到一个类似链表的结构。我们以[2，1，1，3]为例得到下图1：

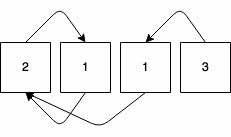
第一个整数为2，则代表它指向index为2的元素，即第二个元素，以此类推。注意由于整数的范围为1到n，所以起始的index为1而不是0。我们从最后一个整数3开始跟随指针的方向前进，依次经过的元素如下图2所示：

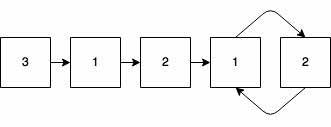
之所以将最后一个元素作为起点，是因为最后一个元素的index为n+1，而最大的整数为n，所以不可能会存在指向最后一个元素的指针。我们发现这个这个链表到最后进入了一种循环的状态，即一个cycle。那是不是对于任意题目中的列表都会发生这种情况呢？答案是肯定的，因为至少存在两个重复的整数，所以一定存在至少两个指针指向同一个位置，并且这个位置就是cycle的起始点。再总结一下：

由于每个整数都代表一个指针，重复的整数将会导致一个位置同时有多个指针指向它。
不可能有指针指向列表中最后一个位置，如果我们从最后一个整数开始跟随指针前进，我们最终会进入一个cycle。
cycle的开始位置的index就是重复的整数。

如果从任意一个位置开始，我们可能立马会陷入一个cycle（例如起点的整数就是自己位置的index的情况），但由于将最后一个整数作为起点，所以不可能会发生这种情况。以下是对于该问题的动态演示(n=9)，橙色为重复的整数，红色为cycle开始的位置，点击Randomise随机生成新的数据。

头脑风暴到这里就结束一大半了，那到底要怎么找出cycle的开始位置呢？在计算机科学中，cycle的检测被称作判圈算法。对于这道题，我们采取以下这种比较容易理解的三部式算法：

进入cycle中：从起始位置(列表中最后一个整数)开始，前进n步，则我们必然已经进入了一个cycle。
找出cycle的长度：保持一个指针不动，另一个指针从该位置开始进行前进，当另一指针回到起始点(即与不动的指针相遇)时所前进的步数就是cycle的长度。
找出cylce的起点：从起始位置(列表中最后一个整数)重新开始，使用两个距离为cycle的长度的指针以同样的步伐同时前进，它们相遇的位置就是cycle的起点，重复的整数即为该位置的index。

Python代码如下：

def find_duplicate_super(int_list):

    n = len(int_list) - 1

    # STEP 1: GET INSIDE A CYCLE
    # start at position n+1 and walk n steps to
    # find a position guaranteed to be in a cycle
    position_in_cycle = n + 1
    for _ in xrange(n):
        position_in_cycle = int_list[position_in_cycle - 1]
        # we subtract 1 from the current position to step ahead:
        # the 2nd *position* in a list is *index* 1

    # STEP 2: FIND THE LENGTH OF THE CYCLE
    # find the length of the cycle by remembering a position in the cycle
    # and counting the steps it takes to get back to that position
    remembered_position_in_cycle = position_in_cycle
    current_position_in_cycle = int_list[position_in_cycle - 1]  # 1 step ahead
    cycle_step_count = 1

    while current_position_in_cycle != remembered_position_in_cycle:
        current_position_in_cycle = int_list[current_position_in_cycle - 1]
        cycle_step_count += 1

    # STEP 3: FIND THE FIRST NODE OF THE CYCLE
    # start two pointers
    #   (1) at position n+1
    #   (2) ahead of position n+1 as many steps as the cycle's length
    pointer_start = n + 1
    pointer_ahead = n + 1
    for _ in xrange(cycle_step_count):
        pointer_ahead = int_list[pointer_ahead - 1]

    # advance until the pointers are in the same position
    # which is the first node in the cycle
    while pointer_start != pointer_ahead:
        pointer_start = int_list[pointer_start - 1]
        pointer_ahead = int_list[pointer_ahead - 1]

    # since there are multiple values pointing to the first node
    # in the cycle, its position is a duplicate in our list
    return pointer_start

4 运行时间测试

我们取n=9999并且只有一个整数重复两次来进行一个简单的测试。

timeit find_duplicate(l)
1 loop, best of 3: 6.48 s per loop

timeit find_duplicate_good(l)
100 loops, best of 3: 6.85 ms per loop

timeit find_duplicate_super(l)
1000 loops, best of 3: 551 µs per loop